生成学习算法

判别学习算法的模型是通过一条分隔线把两种类别区分开，而生成学习算法是对两种可能的结果分别进行建模，然后分别和输入进行比对，计算出相应的概率.

一、引言

我们常用的算法是逻辑回归，判别模型，即找到0和1之间的界限，找到一个决策边界，来区分0和1，而生成学习算法是通过0的特征学习出一个0的模型，根据1的特征学习出一个1的模型，对于一个新的样本，分别放入0 1的模型中，先求得是0的概率，再求是1的概率，进行比较，即可确定类型。这里计算概率使用的是贝叶斯公式。主要完成对$p(x|y)$和$p(y)$的建模

二、高斯判别分析（Gaussian Discriminant Analysis）

假设$p(x|y)$满足多维正态分布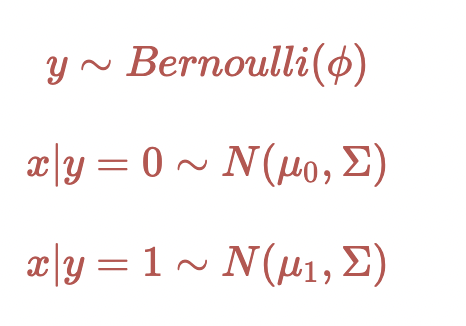

概率分布为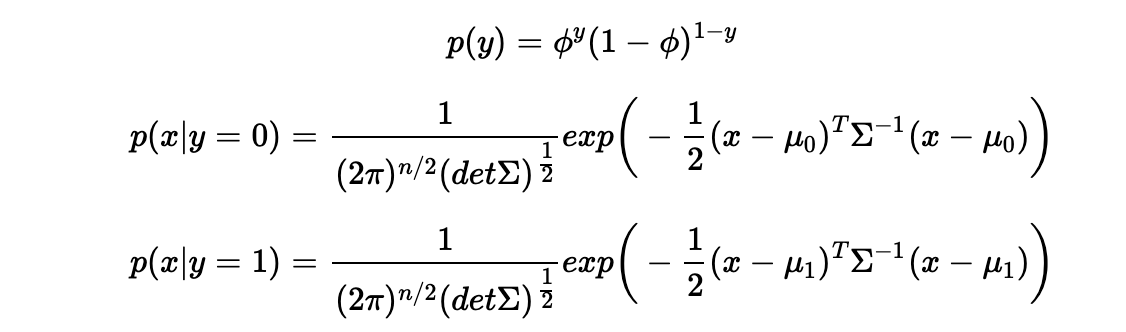

极大似然估计求得所有的参数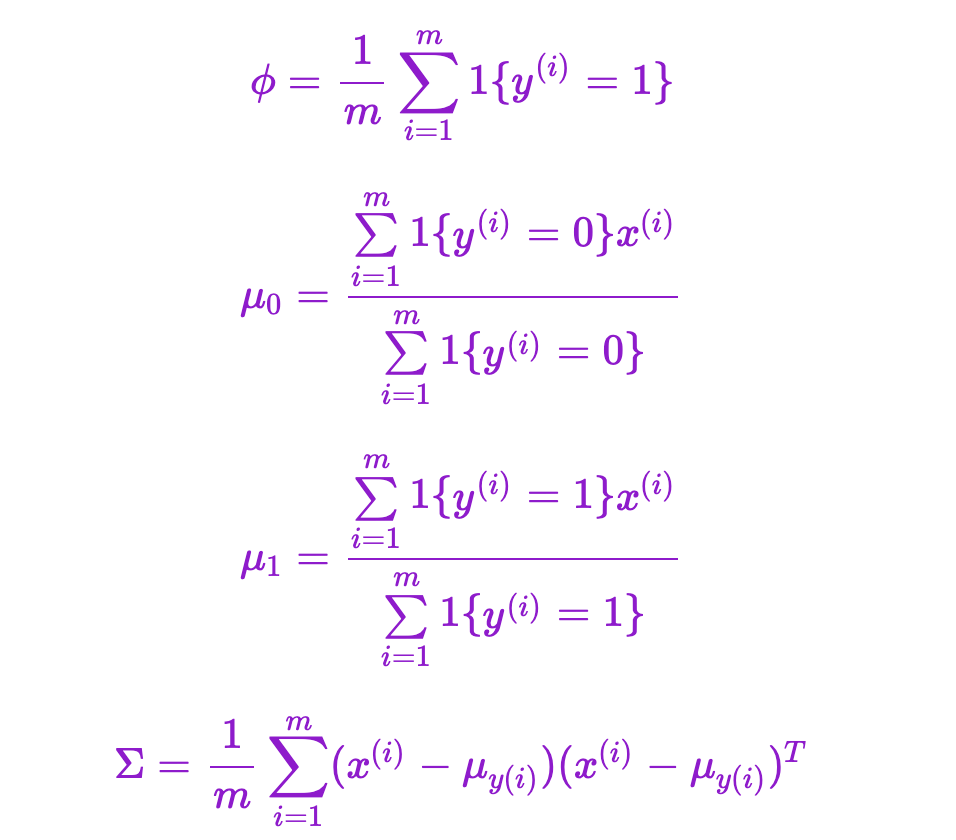

其中，$ϕ$ 是训练样本中结果y=1占有的比例，$μ_0$是y=0的样本中特征均值，$μ_1$ 是y=1的样本中特征均值，$Σ$ 是样本特征方差均值。

注意这里的参数有$μ_0$和$μ_1$，表示在不同的结果模型下，特征均值不同，但我们假设协方差相同。反映在图上就是不同模型中心位置不同，但形状相同。这样就可以用直线来进行分隔判别。

所以我们得到这样的图像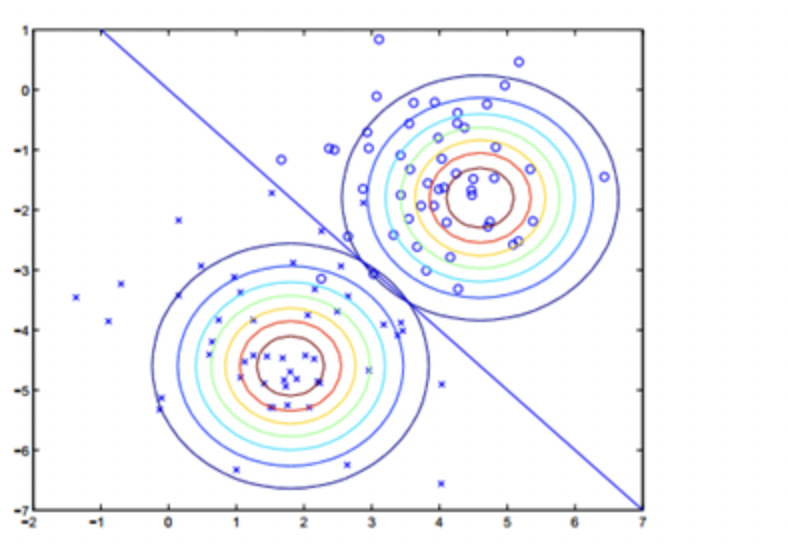

三、朴素贝叶斯（Naive Bayes）

当$x$是离散值时，我们假设垃圾邮件分类的情况。将一封邮件作为输入向量，如果字典中第$i$个词在字典中出现，则$x_i$=1，反之$x_i$=0，这样我们得到所需的特征向量。

现在对$p(x|y)$建模，假设字典中有50000个词，$x \in{0,1}^{50000}$，如果采用多项式建模， 将会有$2^{50000}$种结果，$2^{50000}$−1维的参数向量，这样明显参数过多，很难进行计算。所以为了对$p(x|y)$建模，需要做一个强假设，假设x的特征是条件独立的，这个假设称为朴素贝叶斯假设(Naive Bayes (NB) assumption),这个算法就称为朴素贝叶斯分类(Naive Bayes classifier).

根据概率论的链式法则性质和朴素贝叶斯假设，我们可以得到如下等式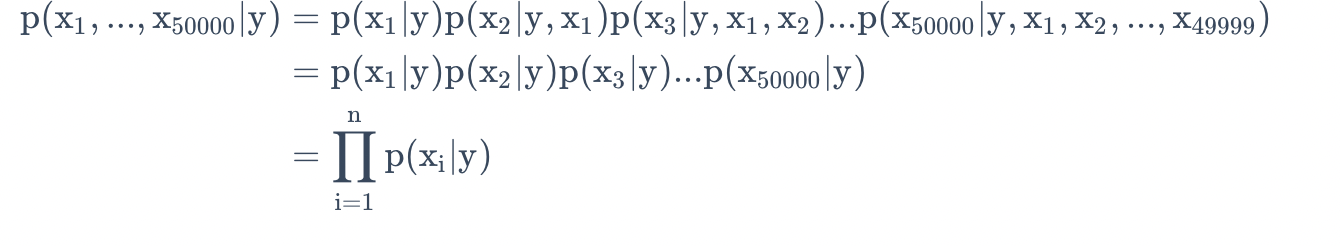

根据联合似然函数，再依次得到参数的最大似然估计值，我们对一个全新的样本进行预测，特征为$x$，则有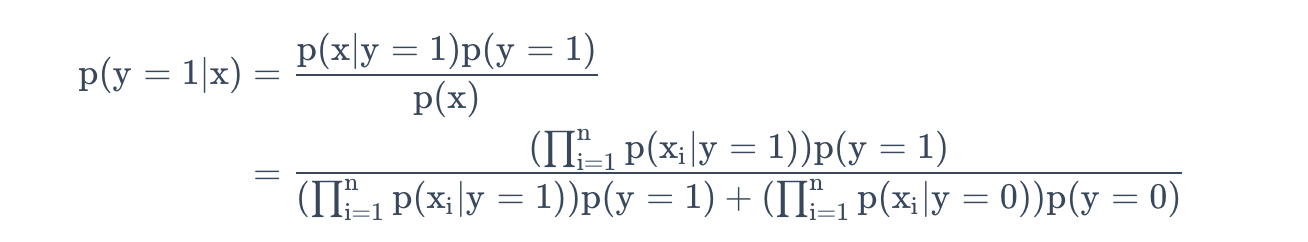

因为分母对于y取0或1是一样的，所以只需要计算比较分子即可确定分类。

四、拉普拉斯平滑（Laplace smoothing）

朴素贝叶斯模型已经能不错的解决离散值的问题，可是对于数据稀疏问题，朴素贝叶斯模型并不能很好的解决，还是针对邮件分类问题，假设收到了一封含有NIPS的邮件，但是NIPS从未在垃圾邮件或者正常邮件中出现过，假设NIPS在字典中位子伟35000，则计算概率时，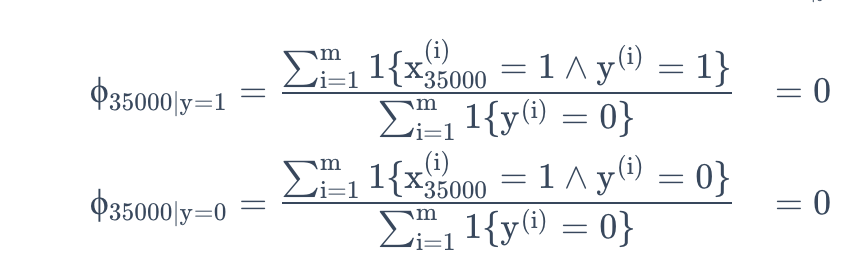
而后验概率计算得到的为$\frac{0}0$，也就不知道该如何预测了。

这里我们引入拉普拉斯平滑，将估计替换为

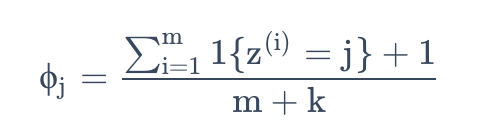
这里首先是对分子加1，然后对分母加k，要注意$\sum^k_{j=1} \phi_j = 1$依然成立（自己检验一下），这是一个必须有的性质，因为$\phi_j$
是对概率的估计，然后所有的概率加到一起必然等于1。另外对于所有的$j$值，都有$\phi_j \neq 0$，这就解决了刚刚的概率估计为零的问题了。在某些特定的条件下（相当强的假设条件下，arguably quite strong），可以发现拉普拉斯平滑还真能给出对参数$\phi_j$ 的最佳估计（optimal estimator）

在朴素贝叶斯问题上，使用拉普拉斯平滑后得到的公式则为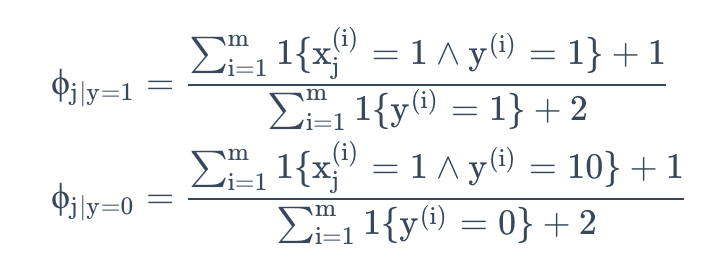

注：在实际应用中，是否对$\phi_y$使用拉普拉斯平滑影响不大，因为$\phi_y$是对$p(y=1)$的一个合理估计，而垃圾邮件与正常邮件是成一定比例的，所以$\phi_y$与零点存在一定的距离。