数学结论

均值不等式

均值不等式证明

整数拆分问题

即将一个数$ $拆分为$k$个数，使得$k$个数乘积最大。

由均值不等式易得$k$个数相等时 乘积是最大的，那么这$k$个数应该等于多少呢？

即求$f(x)=x^{\left(\frac{n}{x}\right)}$的最大值

$f(x)=x^{\left(\frac{n}{x}\right)}=e^{\frac{n}{x} \ln x}$

易得$h(x)=\frac{1}{x} \ln x$ 与$f(x)$有相同的单调性

$h^{\prime}(x)=\frac{1-\ln x}{x^{2}}$

可知，x=e时，$f(x)$取得最大值，由于2不是整数，所以可以是2或3.

则将$n$拆分为尽量多的3以及少量2即可。

总结可得

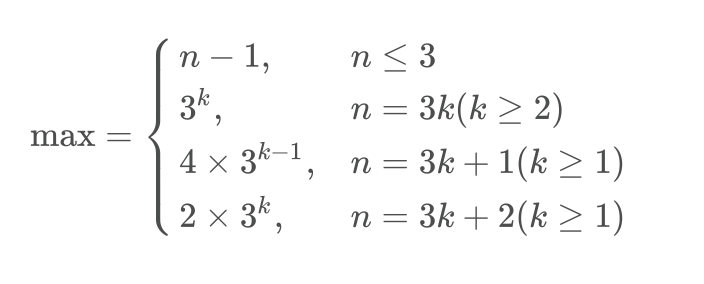
线性代数性质

$$
\operatorname{tr}(A B)=\operatorname{tr}(B A)
$$

证明：
$$
\operatorname{tr}(A B)=\sum_{i=1}^{m}(A B){i i}=\sum{i=1}^{m} \sum_{j=1}^{n} a_{i j} b_{j i}=\sum_{i=1}^{m} \sum_{j=1}^{n} b_{j i} a_{i j}=\sum_{i=1}^{n}(B A)_{i i}=\operatorname{tr}(B A)
$$